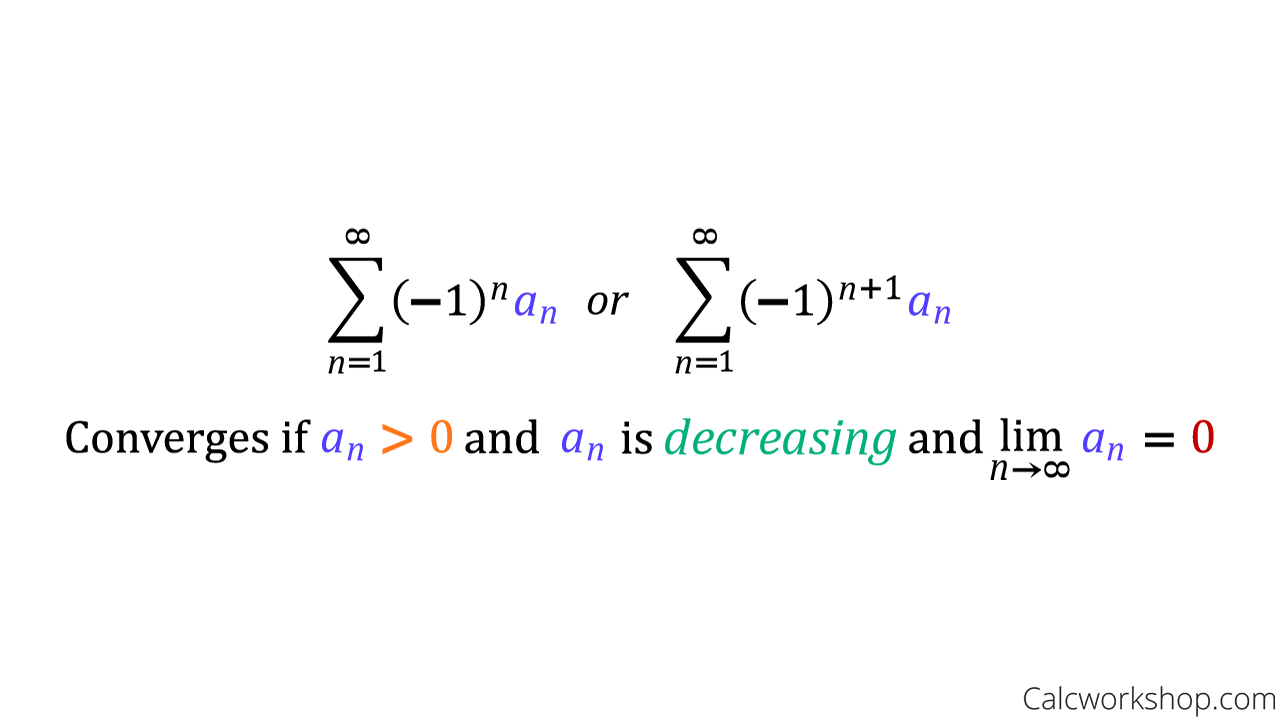SOLVED:The series Za=,(-1Ycoslh _ is Select one: a. Convergent by Alternating Series Test. b. Non of them Absolutely Convergent d Divergent by Alternating Series Test: Divergent by nth-Term Test,
SOLVED:The series Zn =1 (-1y"cos(4) is Select one: ai Divergent by Alternating Series Test. b. Non of them Cr Convergent by Alternating Series Test d. Absolutely Convergent: e Divergent by nth-Term Test;
Alternating Series Test
Solved (1 point) The alternating series test. h +1 We want | Chegg.com
Alternating Series and the Alternating Series Test
Which Convergence Test Should I Use?
Solved (1 point) The alternating series test. 1+1 We want to | Chegg.com
9.5 Alternating Series and Absolute Convergence‣ Chapter 9 Sequences and Series ‣ Calculus II
CC Alternating Series and Absolute Convergence
PPT - The Ratio Test: PowerPoint Presentation, free download - ID:2842021
Converse X Off-White Are Back With A Chuck Taylor Collab | Urban List Sunshine Coast
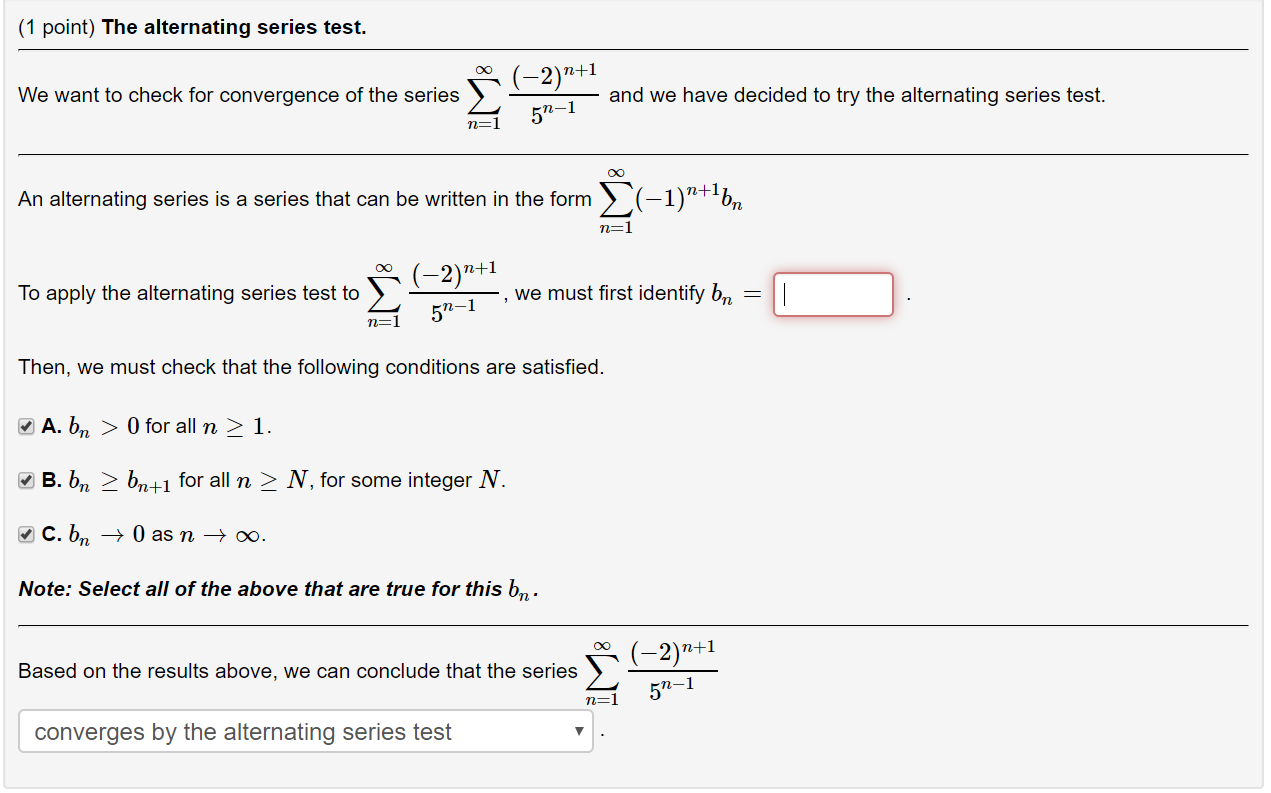
SOLVED:Which of the following are correct conclusions? Choose all that apply C 5 9 = Series is CONVERGENT due to the Geometric Series Test Series is DIVERGENT due to the Geometric Series
Alternating Series
Conditional & absolute convergence (video) | Khan Academy
Alternating Series: Definition & Examples | Study.com
How to Determine Whether an Alternating Series Converges or Diverges - dummies
Alternating Series, Absolute Convergence
Math253 absolute convergence, the ratio test, and power series - Math 253 – absolute convergence, - StuDocu
Alternating Series Test Conditions - Mathematics Stack Exchange
Alternating Series, Absolute Convergence
Chapter VIII
Alternating Series Test. It's the test for Alternating series. | by Solomon Xie | Calculus Basics | Medium
Absolute vs Conditional Convergence Alternating Series and the
Divergent vs absolute and conditionally convergent series | Math, Calculus, Alternating series | ShowMe
Alternating series test question. - Mathematics Stack Exchange
Integral test for convergence - Wikipedia
a review sheet for test #03
PPT - The Integral Test PowerPoint Presentation, free download - ID:3060075
